Grundlagen Statistik & Algorithmen, Teil 4 Der Monte-Carlo-Algorithmus und -Simulationen

Eine Reihe von Algorithmen dient der Suche von Lösungen, ohne vorher die Antwort zu kennen, und von Entscheidungen, die nach „wahrscheinlich richtig oder falsch“ beurteilt werden. Das ist sinnvoll für das Risiko-Management, aber auch für die Nutzung von Supercomputern. Ein solcher Algorithmus ist der Monte-Carlo-Algorithmus und die darauf basierenden Simulationen

Anbieter zum Thema

Fujitsu Technology Solutions GmbH

INFOMOTION GmbH

Im Unterschied zu einem deterministischen Algorithmus, der mit definierten und reproduzierbaren Zuständen arbeitet, arbeitet ein Monte-Carlo-Algorithmus ergebnisoffen mit Zufallswerten. Das klingt zunächst zwar wenig ermutigend, aber der Nutzer arbeitet hier, wie sonst, mit Wahrscheinlichkeiten statt mit Gewissheiten.

Ein Monte-Carlo-(MC)-Algorithmus ist ein randomisierter Algorithmus, der durch die Wahl von zufälligen Zwischenergebnissen zu einem (im Mittel) guten bzw. näherungsweise korrekten Ergebnis gelangen soll. Mit Zufallswerten gefüttert, darf der MC-Algorithmus mit einer nach oben beschränkten Wahrscheinlichkeit ein falsches Ergebnis liefern. Man rechnet also keinesfalls wild drauflos, bis der Welt die Energie ausgegangen ist, sondern hat von vornherein eine Bremse eingebaut.

Wiederholt man den Algorithmus mit unabhängigen Zufallsbits genügend oft, wird sukzessive die Fehlerwahrscheinlichkeit gesenkt. Sinkt sie unter einen vertretbaren Schwellenwert (KPI: Key Performance Indicator), dann ist die Antwort bzw. Entscheidung wahrscheinlich richtig. Der Clou: Der MC-Algorithmus darf ein falsches Ergebnis liefern, sein ebenso randomisierter Bruder, der Las-Vegas-Algorithmus, darf hingegen nur korrekte Lösungen berechnen. Beide lassen sich ineinander konvertieren.

Entscheidungsprobleme

Wie gesagt, gibt es Monte-Carlo-Algorithmen für Suchprobleme (Probleme, bei denen eine Lösung zu berechnen ist) und für Entscheidungsprobleme (Probleme, bei denen eine Ja/Nein-Frage zu beantworten ist). Eine solche Entscheidung könnte die Beurteilung eines eingehenden Datenpakets nach seiner Legitimität und Unschädlichkeit sein, aber auch ein so komplexer Vorgang wie etwa eine Kreditvergabe (im Bereich Risk Management).

Bei Monte-Carlo-Algorithmen für Entscheidungsprobleme unterscheidet man zwischen ein- und zweiseitigen Fehlern. Bei einem zweiseitigen Fehler darf ein Monte-Carlo-Algorithmus sowohl False Positives liefern (also die Ausgabe „Ja“, obwohl „Nein“ richtig wäre), als auch False Negatives (also die Ausgabe „Nein“, obwohl „Ja“ richtig wäre).

Bei einseitigem Fehler ist nur eine der beiden Fehlermöglichkeiten erlaubt. Eine häufige Vereinbarung besteht darin, von einem einseitigen Fehler zu sprechen und damit False Negatives zu meinen. Es gibt dabei drei Komplexitätsklassen für Probleme.

Komplexitätsklassen für Entscheidungsprobleme mit randomisierten Algorithmen

• BPP (von englisch bounded error probabilistic polynomial time): Wenn die korrekte Ausgabe Ja (Nein) lautet, beträgt die Wahrscheinlichkeit, dass der Algorithmus Ja (oder Nein) ausgibt, mindestens 2/3.

• RP (von englisch randomized polynomial time): Wenn die korrekte Ausgabe Ja lautet, beträgt die Wahrscheinlichkeit, dass der Algorithmus Ja ausgibt, mindestens 1/2. Wenn die korrekte Ausgabe Nein lautet, beträgt die Wahrscheinlichkeit, dass der Algorithmus Nein ausgibt, 1.

• co-RP: Wenn die korrekte Ausgabe Ja lautet, beträgt die Wahrscheinlichkeit, dass der Algorithmus Ja ausgibt, 1; wenn die korrekte Ausgabe Nein lautet, beträgt die Wahrscheinlichkeit, dass der Algorithmus Nein ausgibt, mindestens 1/2. Damit enthält co-RP die Komplemente der Probleme in RP. RP und co-RP ergänzen einander.

Wenn ein solcher RP-Algorithmus die Ausgabe Ja liefert, wissen wir mit Sicherheit, dass die Ausgabe Ja korrekt ist (da die Definition sicherstellt, dass bei korrekter Ausgabe Nein dies auf jeden Fall auch ausgegeben wird). Wenn dagegen ein RP-Algorithmus die Ausgabe Nein liefert, wissen wir nichts über die korrekte Ausgabe (da nach der Definition die Ausgabe Nein möglich ist, wenn Ja oder Nein korrekt wäre).

Anwendungsfälle

Der Nutzwert des MC-Algorithmus wird deutlicher, wenn man seine Anwendungsfälle unter die Lupe nimmt. Ein Beispiel ist der Miller-Rabin-Test, bei dem bestimmt wird, ob eine natürliche Zahl eine Primzahl ist. Die Ausgabe des Tests lautet entweder „sicher zusammengesetzt“ oder „wahrscheinlich prim“. Die Wahrscheinlichkeit, dass eine zusammengesetzte Zahl als „wahrscheinlich prim“ klassifiziert wird, liegt pro Durchgang unter 25 Prozent und kann durch mehrfache Ausführung weiter gesenkt werden (sodass mit höherer Wahrscheinlichkeit Primzahlen gefunden werden). Der Miller-Rabin-Test liefert keine Aussage über die Faktoren einer zusammengesetzten Zahl.

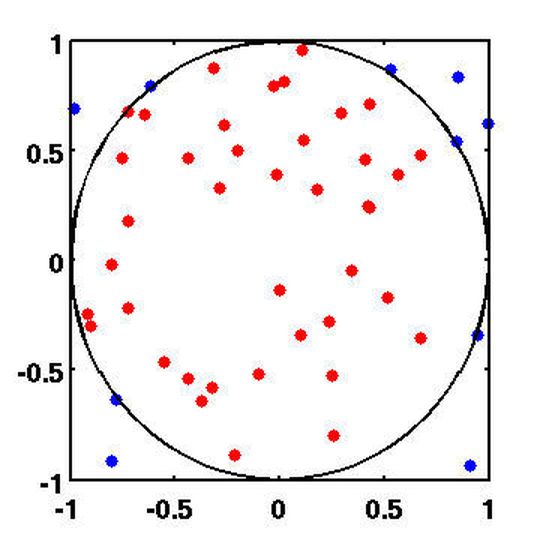
Der Monte-Carlo-Algorithmus lässt sich zur Bestimmung der Kreiszahl Pi heranziehen. Dazu sind die Wahl zufälliger Punkte auf der Kreisfläche und eine sehr komplexe Formel notwendig (siehe Abb. 1). Sie ergibt das Flächenintegral einer Viertelkreisfläche. Aus diesem ergibt sich das Verhältnis von Fläche, Durchmesser und Umfang.

Im Einsatzbereich des Hochleistungsrechnens, das auf massivem Multiprocessing in Parallelverarbeitung über tausende von Prozessorkernen und Rechnerknoten hinweg beruht, lassen sich probabilistische Lösungsverfahren wie der MC-Algorithmus ausnutzen. Zahlreiche Supercomputer in der Top-500-Liste arbeiten deshalb mit Grafikprozessoren (GPU), die für die Parallelverarbeitung optimiert sind.

Monte-Carlo-Simulation

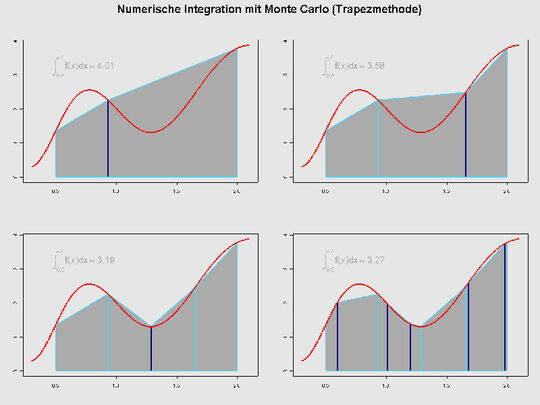
Eine Monte-Carlo-Simulation oder Monte-Carlo-Studie, auch MC-Simulation genannt, ist ein Verfahren aus der Stochastik, bei dem eine sehr große Zahl gleichartiger Zufallsexperimente die Basis darstellt. Auch hier soll die Wahrscheinlichkeitstheorie helfen, aufwendig lösbare Probleme zu beantworten, am denen sich Analyse-Methoden die Zähne ausbeißen würden.

Als Grundlage ist vor allem das Gesetz der großen Zahlen zu sehen. Die Zufallsexperimente können entweder – etwa durch Würfeln – real durchgeführt werden oder in Computerberechnungen. Zur Simulation des Zufalls werden scheinbar zufällig gewählte Zahlen herangezogen und mittels geeigneter Algorithmen wie etwa dem MC-Algorithmus berechnet.

Zu den Anwendungen der MC-Simulation gehören das oben angeführte Beispiel der Bestimmung der Zahl Pi. Die Ermittlung von Verteilungen ist ein eminent wichtiger Bereich in der modernen Wirtschaft, beispielsweise in Werbung, Logistik oder Finanzen. Es lassen sich durch Simulation Zufallsvariablen und Korrelationskoeffizienten ermitteln, die in ihrer Gesamtheit Eingang in eine empirische Verteilungsfunktion finden. Mit dieser Funktion hat man ein alternatives Mittel an der Hand, um Schätzungen für Erwartungswerte vornehmen zu können. Man ist nicht mehr auf das arithmetische Mittel angewiesen und kann zudem die Parameter, die eine Verteilung beeinflussen, schätzen.

Nachbildung komplexer Prozesse

Diese Simulationen helfen bei der Nachbildung komplexer Prozesse wie etwa im Wetter oder im Klima, die sich nicht direkt analysieren lassen. Auch Produktionsprozesse in einem Fertigungsunternehmen sind simulierbar, um Engpässe und Opportunitäten in der Produktion aufzudecken. In der Immobilienwirtschaft lassen sich zwecks Wertermittlung eines Objekts Ableitungen aus bisherigen Bewertungen vornehmen.

Auch an der Börse spielen Simulationen eine zunehmende Rolle, denn dort nimmt die Rechenkapazität ebenso zu wie die Übertragungsgeschwindigkeit der Netzwerke. Wenn beispielsweise keine analytische Formel für die Bewertung eines Finanzproduktes bekannt ist, lassen sich durch MC-Simulation geeignete Verteilungsannahmen der relevanten Zufallsgrößen finden und auf einfache Art komplexe Finanzkontrakte bepreisen. Das ist ungefähr so, als würde man ein Karnickel aus einem Hut zaubern, in den man zuvor nur etwas Feenstaub (die MC-Simulation) gestreut hat.

In letzter Zeit haben besonders die Physik und das darauf basierende Engineering von den Möglichkeiten der MC-Simulation profitiert. Wohin wird sich beispielsweise ein Regentropfen, der auf die Erde fällt, weiterbewegen? Er wird zufällig mit anderen Tropfen gleicher Größe in gleichartiger Umgebung kollidieren. Wird er dabei zerfallen oder sich mit anderen Tröpfchen vereinigen?

Nach der Simulation mehrerer konkreter Tropfen sind Aussagen über die durchschnittliche Tropfengröße möglich oder auch zu Temperatur und Tröpfchendichte, bei denen Schnee oder Hagel entstehen. Das Phänomen der Tröpfchen ist von großer Bedeutung bei der Konstruktion von Einspritzpumpen in Verbrennungsmotoren. An der Universität Stuttgart ist es dadurch gelungen, den Benzinverbrauch eines Verbrennungsmotors um einen zweistelligen Prozentsatz zu senken. Am Höchstleistungsrechenzentrum Stuttgart (HLRS) wird auch in einer Art Rundum-Kino der Zerfall eines Treibstoff-Tropfens als Simulation gezeigt, natürlich in extremer „Zeitlupe“ – ein faszinierender Anblick.

Grundlagen Statistik & Algorithmen, Teil 1

Das Problem des Handlungsreisenden und seine praktischen Anwendungen

Grundlagen Statistik & Algorithmen, Teil 2

So verfeinert das Bayes-Theorem Spam-Filter – und mehr

Grundlagen Statistik & Algorithmen, Teil 3

Speed für Mustererkennung mit dem Rete-Algorithmus

Grundlagen Statistik & Algorithmen, Teil 5

Optimale Clusteranalyse und Segmentierung mit dem k-Means-Algorithmus

Grundlagen Statistik & Algorithmen, Teil 6

Die Ereigniszeitanalyse – wenn Anfang und Ende die Erfolgsrate bestimmen

Grundlagen Statistik & Algorithmen, Teil 7

So deckt der Local Outlier Factor Anomalien auf

(ID:45415245)