Grundlagen Statistik & Algorithmen, Teil 6 Die Ereigniszeitanalyse – wenn Anfang und Ende die Erfolgsrate bestimmen

Die Ereigniszeitanalyse bzw. Survival Analysis umfasst eine Reihe von Werkzeugen der Statistik, mit denen die Zeit bis zum Eintritt eines bestimmten Ereignisses zwischen Gruppen verglichen wird. Auf diese Weise will man die Wirkung von prognostischen Faktoren, einer medizinischen Behandlung oder von schädlichen Einflüssen abschätzen. Bei dem Ereignis kann es sich um etwas so Endgültiges wie den Tod handeln, aber auch um den Verlust einer Arbeitsstelle, eine Scheidung oder einen Beginn, etwa um eine Geburt oder einen Heilungseintritt.

Anbieter zum Thema

Fujitsu Technology Solutions GmbH

Mit dem Sammelbegriff der „Survival- und Ereigniszeitanalyse“ werden eine Reihe von statistischen Verfahren bezeichnet, die der Untersuchung von Zeitintervallen zwischen aufeinander folgenden Ereignissen oder Zustandswechseln dienen. Die von den Untersuchungseinheiten wie etwa Individuen, Haushalten oder Organisationen eingenommenen Zustände sind dabei stets abzählbar.

In der Regel handelt es sich um eine relativ begrenzte Anzahl von Zuständen wie etwa hohe/tiefe Körpertemperatur, hohe/niedrige Feuchtigkeit usw. Die erfassten Ereignisse können zu beliebigen Zeitpunkten eintreten, bezeichnen aber für gewöhnlich einen Anfangs- oder Endpunkt, wie etwa eine Geburt, eine Inbetriebnahme, eine Heilung, eine Erkrankung oder das Lebensende – auch das einer Maschine.

Anwendungsfelder

Weil die Ereigniszeitanalyse in der Soziologie und in den Ingenieursdisziplinen so vielfältig verwendbar ist, lassen sich zahlreiche Beispiele für solche Prozesse finden. So sind etwa die Dauer der Arbeitslosigkeit bis zum Beginn einer neuen Erwerbstätigkeit für die Arbeitsmarktforschung interessant. Die Zeit in einer beruflichen Tätigkeit bis zu einem sozialen Aufstieg ist für die soziale Mobilitätsforschung von Interesse. Die Dauer bis zu einem Umzug an einen anderen Ort ist für die Migrationsforschung relevant. Die Ehedauer bis zur Scheidung taucht in der demografischen Forschung auf und die Überlebenszeiten von Patienten werden in medizinischen Studien erfasst.

Analog dazu lassen sich Maschinen beschreiben, etwa im Smart Grid, in einer komplexen Maschine oder in einem sensorgestützten IoT-System. Deshalb wird das Verfahren im Englischen auch „Reliability Theory“, also Zuverlässigkeitsanalyse, genannt. Üblicherweise werden nur Ereignisse untersucht, die höchstens ein Mal pro Subjekt bzw. Gruppe auftreten können, etwa eine Lebenszeit. Eine Erweiterung auf wiederholt auftretende Ereignisse ist indes möglich.

Statistische Funktionen

Es geht stets darum, zentrale Kenngrößen wie etwa die Überlebensrate einer Gruppe oder die Zuverlässigkeit einer Maschine herauszufinden. Daraus folgt, dass die Überlebensfunktion S analog zur Zuverlässigkeitsfunktion R(t) berechnet wird, wobei der Faktor t Zeit ist und P die Höhe der Wahrscheinlichkeit: S(t) = R(t) = P (T>t). T ist die verbleibende Dauer zum Lebensende eines Organismus oder zum Ausfall eines Geräts. Normalerweise ist S(0) = 1, sonst kann nämlich ein sofortiger „Tod“ oder Geräteausfall eintreten.

Aus der Überlebensfunktion lassen sich verschiedene Größen ableiten. Die Ereigniszeit-Verteilungsfunktion, in technischem Bezug auch als Ausfallswahrscheinlichkeit („Probability of failure“) bezeichnet und mit F abgekürzt, ist die komplementäre Funktion zur Überlebensfunktion: F(t). Die erste Ableitung von F, die Ereignisdichtefunktion oder Ausfallsdichte („failure density function“), wird mit f bezeichnet. Die Ereignisdichtefunktion ist die Rate des betrachteten Ereignisses pro Zeiteinheit.

Die Ausfallrate, auch als Hazardfunktion bezeichnet und mit h(t) bezeichnet, ist definiert als Häufigkeit, mit der ein Ereignis zum Zeitpunkt T eintritt, vorausgesetzt, dass es bis zum Zeitpunkt t noch nicht eingetreten ist. Der englische Ausdruck „force of mortality“ (Sterblichkeitsrate) wird speziell in der Demografie verwendet. Die Hazardfunktion kann anwachsen oder fallen, sie braucht weder monoton noch stetig zu sein.

Die verbleibende Lebenszeit zu einem Zeitpunkt t0 ist die bis zum Tod bzw. Ausfall verbleibende Zeit, also T - t0. Die zukünftige Lebenserwartung ist der Erwartungswert der verbleibenden Lebenszeit. Für t0 = 0 reduziert sich dies auf die Lebenserwartung bei der Geburt. In Zuverlässigkeitsanalysen wird die Lebenserwartung englisch „mean time to failure“ (MTTF) und die zukünftige Lebenserwartung englisch „mean residual lifetime“ (MRL) genannt. MTFF ist eine obligatorische Angabe für jede Art von elektrischem oder elektronischem Gerät. Nach Ablauf dieses „Mindesthaltbarkeitsdatums“ sollte das Gerät ausgetauscht werden.

Weitere Methoden

Die statistischen Methoden der Ereigniszeitanalyse reichen von den deskriptiven Verfahren der Survivalanalyse (z. B. Sterbetafel-Methode und Kaplan-Meier-Schätzung), über das semiparametrische Regressionsmodell von Cox, bis zu den parametrischen Verfahren mit und ohne Zeitabhängigkeiten, so etwa dem Exponential-, Piecewise-Constant-, Gompertz (-Makeham)-, Weibull- oder log-logistischen Modell. Im begrenzten Rahmen dieses Beitrag können nur der Kaplan-Meier-Schätzer und das Cox-Modell näher vorgestellt werden.

Kaplan-Meier-Schätzer (KMS)

Der Kaplan-Meier-Schätzer-Algorithmus, bereits 1958 formuliert, ist eine der am häufigsten verwendeten Methoden der „Survival Analysis“ und in praktisch jedem Statistikpaket (SAS, R, Mathematica, Python usw.) zu finden. Der KMS dient zum Schätzen der Wahrscheinlichkeit, dass bei einem Versuchsobjekt ein bestimmtes Ereignis innerhalb eines Zeitintervalls nicht eintritt.

Es handelt sich um eine nichtparametrische Schätzung der Überlebensfunktion (s.o.) im Rahmen der Ereigniszeitanalyse. Der KMS lässt sich beispielsweise nutzen, um die Sterbewahrscheinlichkeit eines Patienten oder die Ausfallwahrscheinlichkeit eines Geräts zu kalkulieren.

Für eine KM-Verlaufskurve sind zwei Daten nötig: der Status der letzten Messung bzw. Beobachtung und die Zeit bis zum Ereignis. Sollen die Überlebensfunktionen zweier Gruppen verglichen werden, wird ein drittes Datum benötigt: die Gruppenzuordnung jeden Subjekts. Auf diese Daten braucht man nur noch die KM-Formel anwenden.

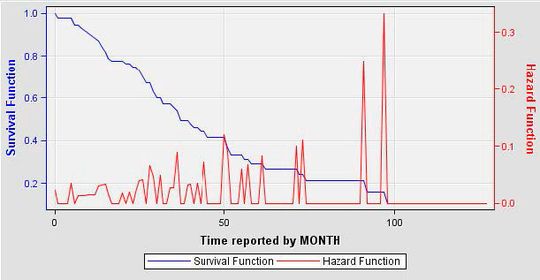
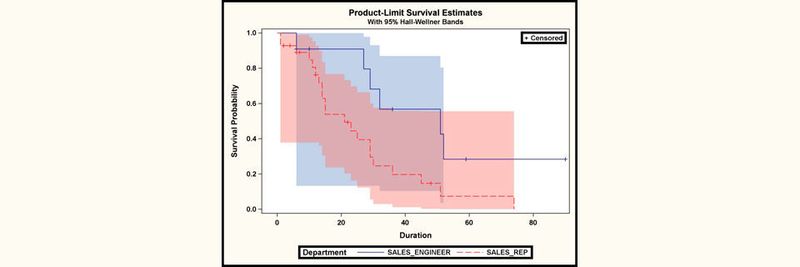
Das Verlaufsdiagramm eines KM-Schätzers (siehe Abbildungen) besteht aus einer Reihe von absteigenden horizontalen Schritten bzw. Stufen, welche, eine ausreichend große Datenmenge vorausgesetzt, sich der wahren Überlebensfunktion (s. o.) dieser Bevölkerungsgruppe annähert. Der Wert der Überlebensfunktion zwischen aufeinanderfolgenden Messungen bzw. Beobachtungen wird als konstant angenommen.

Ein großer Vorteil dieser KM-Kurve besteht darin, dass die Methode auch manche Arten von zensierten Daten berücksichtigen kann, besonders rechts zensierte. Häufig werden Daten nämlich links oder rechts zensiert. Wenn Geburt und Tod bekannt sind, dann ist in diesem Fall der Lebensverlauf eindeutig. Wenn man dagegen nur weiß, dass die Geburt vor einem bestimmten Zeitpunkt stattfand, dann nennt man diesen Datensatz links zensiert.

Genauso könnte nur bekannt sein, dass der Tod nach einem bestimmten Datum eintrat. Das ist dann ein rechts zensierter Datensatz. Ein Lebenslauf kann auf diese Weise auch rechts und links zensiert sein (intervallzensiert). Falls eine Person, die ein bestimmtes Alter nicht erreicht, überhaupt nicht beobachtet wird, dann ist der Datensatz abgeschnitten (engl.: truncated). Bei einem links zensierten Datensatz weiß man dagegen zumindest, dass das Individuum existierte.

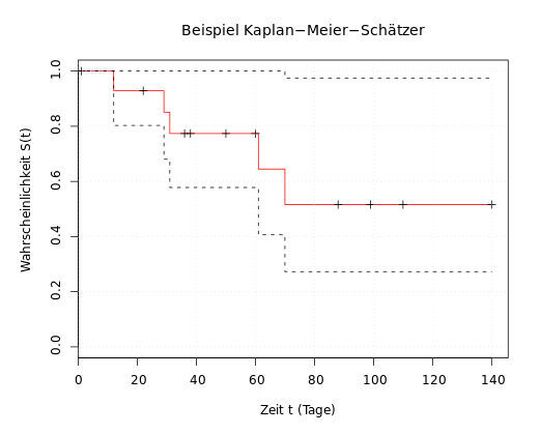
Im Verlaufsdiagramm zeigen kleine Häkchen an, dass einzelne Patienten Überlebenszeiten aufweisen, die rechts-zensiert wurden. Um die Verlässlichkeit auszudrücken, ist im KM-Schätzer das Konfidenzintervall eingeführt worden. Ein Konfidenzintervall ist ein Intervall aus der Statistik, das die Präzision der Lageschätzung eines Parameters angeben soll. Das Konfidenzintervall gibt den Bereich an, der bei unendlicher Wiederholung eines Zufallsexperiments mit einer gewissen Wahrscheinlichkeit die wahre Lage des Parameters einschließt. Das Konfidenzintervall kann aus der Varianz bzw. dem Standardfehler berechnet werden.

Regressionsmodell von Cox

Die Cox-Regression ist eine nach David Cox benannte Regressionsanalyse zur Modellierung von Überlebenszeiten. Wie alle ereigniszeitanalytischen Methoden ist sie ein Verfahren zur Schätzung des Einflusses unabhängiger Variablen auf die Dauer bis zum Eintreten von Ereignissen („Überlebenszeit“) bzw. deren Hazard. Als sogenanntes semiparametrisches Verfahren liefert die Cox-Schätzung kein komplettes Vorhersagemodell für die Überlebenszeit, sondern lässt die Verteilungsfunktion der beobachteten Episodenenden unspezifiziert. Sie schätzt ausschließlich den Einfluss metrischer oder kategorialer Variablen auf einen Baseline-Hazard, von dem angenommen wird, dass er über alle Fälle hinweg konstant ist.

Die Anwendungsgebiete sind ähnlich wie in der Ereigniszeitanalyse. Das von Cox vorgeschlagene Regressionsmodell wird zur Untersuchung des Verhaltens der Ausfallraten in Abhängigkeit von Umwelteinflüssen benutzt, beispielsweise von Soldaten unter Beschuss. Grundlage des Modells sind die Einflussvektoren z von i, mit i = 1 bis n, die für jedes Individuum der Studie beobachtet werden können. Der Zusammenhang zwischen diesen Einflüssen und der Ausfallfunktion wird dann über eine festgelegte Relation h hergestellt.

H von 0 bezeichnet dabei eine unbekannte Ausfallfunktion, die im Ausgangsfall ohne Einflüsse die zugehörige Ausfallfunktion darstellt. ß ist ein unbekannter Parameter, ebenfalls n-dimensional. Aufgabe der Statistik ist die Schätzung dieses Parameters.

Da Jahrzehnte seit der Konzeption dieser beiden Methoden vergangen sind, wurden sie im Laufe der Zeit erweitert, verfeinert und modifiziert. So ist es dem Statistiker möglich, zahlreiche vom Standard abweichende Fälle zu berechnen. In jüngster Zeit kommt den Methoden der Ereignisanalyse eine besondere Bedeutung bei der Weiterentwicklung der Kausalanalyse, der Untersuchung von parallelen und interdependenten Prozessen und der Mehrebenenanalyse zu. Sicher ist aber, dass die Ereigniszeitanalyse mit bedeutenden Algorithmen arbeitet, die in keinem Statistikpaket fehlen dürfen.

Grundlagen Statistik & Algorithmen, Teil 1

Das Problem des Handlungsreisenden und seine praktischen Anwendungen

Grundlagen Statistik & Algorithmen, Teil 2

So verfeinert das Bayes-Theorem Spam-Filter – und mehr

Grundlagen Statistik & Algorithmen, Teil 3

Speed für Mustererkennung mit dem Rete-Algorithmus

Grundlagen Statistik & Algorithmen, Teil 4

Der Monte-Carlo-Algorithmus und -Simulationen

Grundlagen Statistik & Algorithmen, Teil 5

Optimale Clusteranalyse und Segmentierung mit dem k-Means-Algorithmus

Grundlagen Statistik & Algorithmen, Teil 7

So deckt der Local Outlier Factor Anomalien auf

(ID:45704766)